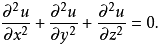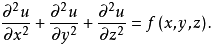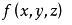10、点云配准
随着计算机辅助设计技术的发展,通过实物模型产生数字模型的逆向工程技术由于它的独特魅力获得了越来越广泛的应用,与此同时,硬件设备的日趋完善也为数字模型操作提供了足够的技术支持。在逆向工程、计算机视觉、文物数字化等领域中,由于点云的不完整、旋转错位、平移错位等,使得要得到完整点云就需要对局部点云进行配准。为了得到被测物体的完整数据模型,需要确定一个合适的坐标变换,将从各个视角得到的点集合并到一个统一的坐标系下形成一个完整的数据点云,然后就可以方便地进行可视化等操作,这就是点云数据的配准。点云配准有手动配准、依赖仪器的配准和自动配准。通常我们所说的点云配准技术即是指最后一种自动配准。点云自动配准技术是通过一定的算法或者统计学规律,利用计算机计算两块点云之间的错位,从而达到把两片点云自动配准的效果。其实质是把在不同的坐标系中测量得到的数据点云进行坐标变换,以得到整体的数据模型。问题的关键是如何求得坐标变换参数RC旋转矩阵和TC平移向量,使得两视角下测得的三维数据经坐标变换后的距离最小。(跟测量学的自由移站法原理一样)目前,配准算法按照实现过程可以分为整体配准和局部配准。PCL中有单独的配准模块,实现了配准相关的基础数据结构与经典配准算法如ICP等,以及配准过程中的对应点估计、错误对应点去除等流程。
PCL中实现的配准算法以及相关概念如下:
(1)两两配准简介(pairwise registration)
一对点云数据集的配准问题是两两配准(pairwise registration 或 pair-wise registration).通常通过应用一个估计得到的表示平移和旋转的4*4刚体变换矩阵来使得一个点云的数据集精确的与另一个点云数据集(目标数据集)进行完美的配准。四参数法。
具体的实现步骤:
①首先从两个数据集中按照同样的关键点选取的标准,提取关键点
②对选择所有的关键点分别计算其特征描述子
③结合特征描述子在两个数据集中的坐标位置,以两者之间的特征和位置的相似度为基础,来估算它们的对应关系,初步的估计对应点对。
④假设数据是有噪声,去除对配准有影响的错误的对应点对。
⑤利用剩余的正确的对应关系来估算刚体变换,完整配准。
(2)对应估计(correspondences estimation)
假设我们已经得到由两次扫描的点云数据获得的两组特征向量,在此基础上,我们必须找到,相似特征再确定数据的重叠部分,然后才能进行配准,根据特征的类型PCL使用不同的方法来搜索特征之间的对应关系
使用点匹配时,使用点的XYZ的坐标作为特征值,针对有序点云和无序点云数据的不同的处理策略:
①穷举配准(brute force matching)
②kd树最近邻查询(FLANN)
③在有序点云数据的图像空间中查找
④在无序点云数据的索引空间中查找
进行特征匹配时(不使用点的坐标,而是某些由查询点邻域确定的特征,如法向量、局部或全局 形状直方 图等),有以下几种方法:
①穷举配准(brute force matching)
②kd树最近邻查询(FLANN)
除了查询之外, 对应估计也区分了两种类型:
①直接对应估计(默认):为点云A中的每一个点搜索点云B中的对应点,确认最终对应点对。
②“相互”(Reciprocal)对应估计:首先为点云A中的点到点云B搜索对应点,然后又从点云B到点云A搜索对应点,最后只取交集作为对应点对。
所有这些在 PCL 类设计和实现中都 以函数 的形式让用户可以自由设定和使用。
(3)对应关系的去除(correspondence rejection)
由于噪声的影响,通常并不是所有估计的对应关系都是正确的,由于错误的对应关系对于最终的刚体变换矩阵的估算会产生负面的影响,所以必须去除它们,可以采用随机采样一致性估计,或者其他方法剔除错误的对应关系,最终使用对应关系数量只使用一定比例的对应关系,这样既能提高变换矩阵的估计精度也可以提高配准点的速度。
遇到有一对多对应关系的特例情况,即目标模型中的一个点对应源中的若干个点与之对应。可以通过只取与其距离最近的对应点或者检查附近的其他匹配的滤波方法过 滤掉其他伪对应关系。 同样地针对对应关系的去除PCL有单独设计类与之对应。
(4)变换矩阵估算(transformation estimation)
估算 变换矩阵步骤如下:
①在对应关系的基础上评估一些错误的度量标准。
②在摄像机位姿(运动估算 )和最小化错误度量标准下估算一个(刚体)变换。
③优化点的结构。
④使用刚体变换把源旋转/平移到于目标所在的同一坐标系下,用所有点、点的一个子集或者关键点运行一个内部ICP循环。
⑤进行迭代,直到符合收敛性判断标准为止。
(5)选代最近点算法(Iterative Closest Point,简称ICP算法)
ICP算法对待拼接的2片点云,首先根据一定的准则确立对应点集P与Q,其中对应点对的个数为n,然后通过最小二乘法迭代计算最优的坐标变换,即旋转矩阵R和平移矢量T,使得误差函数最小。ICP算法计算简便直观且可使拼接具有较好的精度,但是算法的运行速度以及向全局最优的收敛性却在很大程度上依赖于给定的初始变换估计以及在迭代过程中对应关系的确立。 各种粗拼接技术可为 ICP 算法提供较好的初始位置,所以迭代过程中确立正确对应点集以避免迭代陷入局部极值成为各种改进算法的关键,决定了算法的收敛速度与最终的拼接精度。 ICP 处理流程分为4个主要步骤:①对原始点云数据进行采样;②确定初始对应点集;③去除错误对应点对;④坐标变换的求解。
(6)采样一致性初始配准算法(简称SAC-IA算法)
配准算法从精度上分两类:一种是初始的变换矩阵的粗略估计,另一种是像 ICP一样的精确的变换矩阵估计。 对于初始的变换矩阵粗略估计,贪婪的初始配准方法工作量很大,它使用了点云数据旋转不变的特性。 但计算复杂度较高,因为在合并的步骤需要查看所有可能的对应关系。 此外,因为这是一个贪婪算法,所以有可能只能得到局部最优解。 因此我们采用采样一致性方法,试图保持相同的对应关系的几何关系而不必尝试了解有限个对应关系的所有组合。 相反,我们从候选对应关系中进行大量的采样并通过以下的步骤对它们中的每一个进行排名。
①从P中选择s个样本点,同时确定他们的配对距离大于用户设定的最小 值dmin
②对于每个样本点,在Q找到中找到满足直方图和样本点直方图相似的点存入一个列表中。 从这些点中随机选择一些代表采样点的对应关系。
③计算通过采样点定义的刚体变换和其对应变换,计算点云的度量错误来评价转换的质量。我们计划通过查看非常大量的对应关系,快速找到一个好的变换。
重复这3个步骤直至取得储存了最佳度量错误,并使用暴力配准部分数据。 最后使用一个 Levenberg-Marquardt 算法进行非线性局部优化。
莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)能提供数非线性最小化(局部最小)的数值解。此算法能借由执行时修改参数达到结合高斯-牛顿算法以及梯度下降法的优点,并对两者之不足作改善(比如高斯-牛顿算法之反矩阵不存在或是初始值离局部极小值太远)
总之,就是找到两个数据集的对应关系,使得两个数据集的点距平方和最小(或者说点的方差最小)。
11、点云分割(Segmentation)
点云分割是根据空间、几何和纹理等特征对点云进行划分,使得同一划分内的点云拥有相似的特征。 点云的有效分割往往是许多应用的前提,例如,在逆向工程CAD/CAM 领域对零件的不同扫描表面进行分割,然后才能更好地进行孔洞修复、 曲面重建、特征描述和提取,进而进行基于3D内容的检索、组合重用等。 在激光遥感领域,同样需要对地物首先进行分类处理,然后才能进行后期地物的识别、重建。
总之,分割采用分而治之的思想在点云处理中和滤波一样属于重要的基础操作,在PCL 中目前实现了进行分割的基础架构,为后期更多的扩展奠定了基础,现有实现的分割算法是鲁棒性(robust)比较好的聚类分割和基于随机采样致性的分割。
(1)聚类分割算法
在聚类方法中每个点都与一个特征向量相关联,特征向量又包含了若干个几何或者辐射度量值。 然后,在特征空间中通过聚类的方法(如 K-mean 法、最大似然方法和模糊聚类法)分割点云数据。 聚类分割的基本原理为:考察m个数据点,在m维空间内定义点与点之间某种性质的亲疏聚类,设m个数据点组成n类,然后将具有最小距离的两类合为一类,并重新计算类与类之间的距离,迭代直到任意两类之间的距离大于指定的阀值,或者类的个数小于指定的数目,完成分割。
(2)基于随机采样致性(RANSAC)的分割
基于随即一致性算法的分割是通过随机取样剔除局外点,构建仅由局内点数据组成的基本子集的过程。其基本思想为:在进行参数估计时,不是不加区分地对待所有可能的输入数据,而是首先针对具体问题设计出一个判断准则模型,利用此判断准则迭代地剔除那些与所估计的参数不一致的输入数据,然后通过正确的输入数据来估计模型参数。 基于随机采样一致性的点云分割的过程为:首先从输入的点云数据集中随机选择一些点并计算用户给定模型的参数,对数据集中的所有点设置距离阀值,如果点到模型的距离在距离阀值范围内,则将该点归为局内点,否则为局外点,然后统计所有局内点的个数,判断是否大于设定的阔值,如果是,则用内点重新估计模型,作为模型输出,存储所有内点作为分割结果,如果不是,则与当前最大的局内点个数对比,如果大于则取代当前最大局内点个数,并存储当前的模型系数,然后进行迭代计算,直到分割出用户满意的模型。
12、曲面重建(Surface)
曲面重建技术在逆向工程、数据可视化、机器视觉、虚拟现实、医疗技术等领域中得到了广泛的应用。 例如,在汽车、航空等工业领域中,复杂外形产品的设计仍需要根据手工模型,采用逆向工程的手段建立产品的数字化模型;根据测量数据建立人体以及骨髓和器官的计算机模型在医学、定制生产等方面都有重要意义。 除了上述传统的行业,随着新兴的廉价RGBD获取设备在数字娱乐行业的病毒式扩展,使得更多人开始使用点云来处理对象并进行工程应用。 根据重建曲面和数据点云之间的关系可将曲面重建分为两大类:插值法和逼近法。 前者得到的重建曲面完全通过原始数据点,而后者则是用分片线性曲面或其他形式的曲面来逼近原始数据点,从而使得得到的重建曲面是原始点集的一个逼近。 而根据重建曲面的表现形式不同又可以将它分为以下5种:参数曲面重建、隐式曲面重建、变形曲面重建、细分曲面重建和分片线性曲面重建。 PCL中目前实现了基于点云的曲面重建模块框架,在此基础上实现了比较基础的泊松重建、MC重建、EarClipping等算法。
(1)voronoi图概念
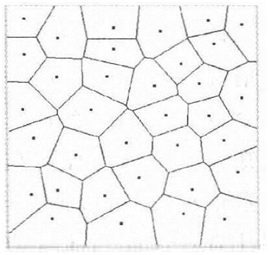
voronoi图是对平面内n个离散点而言的,它是由连接这n个离散点中相邻两点直线的垂直平分线所组成的连续多边形组成,它将平面分为几个区,每个区包括一个点,该点所在区域是到该点距离最近点的集合。下图即为voronoi图的示例图。
voronoi图
(2)Ear clipping三角化算法
Ear clipping是一个多边形三角化的算法。多边个顶点和它相邻两个顶点可以组成形的一个三角形,如果这个三角形内部不存在这个多边形的其他顶点,就可以把这个由该顶点及它相邻点组成的三角形当做一个ear,并沿那两个相邻顶点切下这个ear,每切一次能得到一个三角形和一个少了一个顶点的多边形,重复上述操作,直到该多边形只剩3个顶点。这样,这个多边形被完全分解为三角形
(3)贪婪投影三角化算法(Greedy Projection Triangulation)
将三维点通过法线投影到某一平面,然后对投影得到的点云作平面内的三角化从而得到各点的连接关系。 在平面区域三角化的过程中用到了基于Delaunay的空间区域增长算法,该方法通过选取一个样本三角片作为初始曲面,不断扩张曲面边界,最后形成一张完整的三角网格曲面。 最后根据投影点云的连接关系确定各原始三维点间的拓扑连接,所得三角格网即为重建得到的曲面模型。
贪婪投影三角化算法是一种对原始点云进行快速三角化的算法。 该算法假设 面光滑,点云密度变化均匀,不能在三角化的同时对曲面进行平滑和孔洞修复。
(4)移动立方体算法(MarchingCubes,MC)
移动立方体算法的基本思想就是找出所有与等值面相交的体素,再分别找出每个体素与等值面相交的交面,这些交面连在一起就是所求的等值面。
将点云所在区域用平均单元格进行空间划分后,每上下相对应的八个点构成一个立方体,称为Cube,也可以称做Cell、Voxel 等。 该立方体为体素,为了确定体素中等值面的剖分方式,要为所求等值面规定一个极限值,然后对体素的8个顶点进行分类,来判定顶点是位于等值面之内还是位于等值面之外,再根据顶点分类结果确定等值面的剖分方式。
顶点分类规则如下:
①如果顶点的数据值大于等值面的值,则定义该顶点位于等值面之内。
②如果顶点的数据值小于等值面的值,则定义该顶点位于等值面之外。
当一个体素中一些顶点的值大于阀值(即等值面极限值),而另 一些顶点值小于阀值,那么等值面必然通过这个体素,一个体素的8个顶点的值全都小于阀值或者全都大于阀值的话,那么该体素不与等值面相交,等值面不通过该体素。
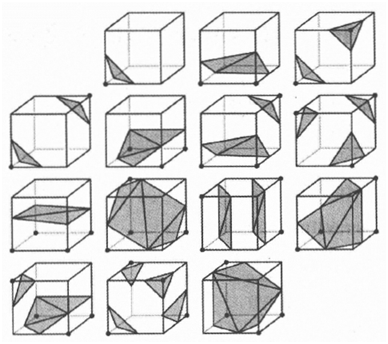
当确定等值面通过该体素后,由于共有8个顶点,每个顶点都有在等值面内或外两种情况,所以一共有256种组合方式,每一种组合都对应一种剖分方式,然而又因为8个点有对称关系,所以256种组合可以简化为下图所示的15种组合。
知道了等值面如何与体素相交后就可以求得等值面与体素边界交点,即等值点。一假设可以用线性当体素很小时,可以假定函数沿体素边界呈线性变化,因此根据这一假设可以用线性插值计算等值面与体素边界的交点。求出等值点以后,就可以根据那15种剖分方式将这些等值点连接成三角形或多边形,再将得到的三角形和多边形连接,就得到等值面。
MC算法15种剖分
(5)泊松曲面重建算法
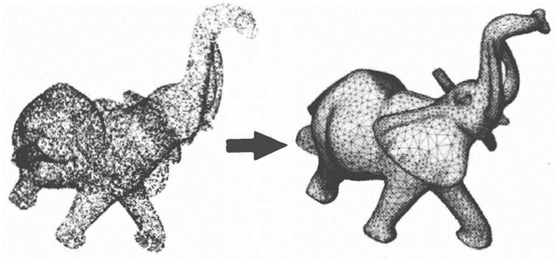
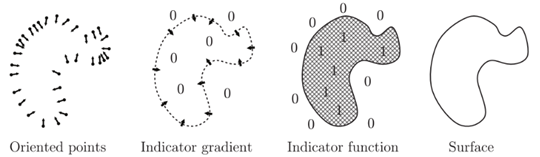
泊松曲面重建法是一种基于隐式函数的三角网格重建算法,该类方法通过对点云数据进行最优化的插值处理来获得近似曲面。泊松曲面重建的具体方法及实现过程:算法输入数据S是一个样本集,每个样本包含一个点p和一个内法线N,即输入数据为包含法线的点云数据,假设所有点位于或者邻近一个未知模型的表面(设为M)。 算法目标是估计模型的指示函数和提取等值面,再基于指示函数和等值面利用MC算法完成曲面重建,最终输出为曲面模型数据,如下图所示
泊松算法重建
拉普拉斯方程
此方程用于描述无源静电场的电位,引力场,弹性薄膜的平衡位移,不可压缩流体的速度场,稳态热传导问题的温度分布和其它诸多物学现象。
泊松方程
式中
为一个描述场源或场漏的给定函数。这是非齐次的拉普拉斯方程。泊松方程表示有源或有漏的情况下拉普拉斯方程描述的物学现象。
采样数据重构方法
关于采样数据的重构有基于组合结构和基于隐函数两类方法。
基于组合结构的方法, 如 Delaunay triangulations, alpha shapes 或Voronoi diagrams 这些方法通过建立三角形网格插值所有或大多数点。当存在噪声点时,所产生的表面往往是锯齿状,因此需要平滑或对数据进行处理(refit to the points in subsequent processing)。
隐函数方法则通过定义分段函数, 定义模型内部的值大于零, 模型外部它的值小于零, 然后提取值为零的等值面, 这类方法可以直接地重构逼近表面, 如基于快速傅立叶转换和径向基函数(RBFs ) 的重构方法都属于隐函数重构方法。
泊松曲面重建属于隐函数方法实现。泊松表面重建的算法融合了全局和局部方法的优点,采取隐性拟合的方式,通过求解泊松方程来取得点云模型所描述的表面信息代表的隐性方程,通过对该方程进行等值面提取,从而得到具有几何实体信息的表面模型。优点在于,重建出的模型具有水密性的封闭特征,具有良好的几何表面特性和细节特性。
整个算法的步骤包括对具有法向量信息的输入点云信息的预处理,对全局问题离散化,对离散化后的子数据求解,求解泊松问题后的等值面提取,以及后期优化处理等。
表面重建过程
1、定义八叉树。使用八叉树结构存储点集,根据采样点集的位置定义八叉树,然后细分八叉树使每个采样点都落在深度为D的叶节点;
2、设置函数空间:对八叉树的每个节点设置空间函数F,所有节点函数F的线性和可以表示向量场V,基函数F采用了盒滤波的n维卷积;
3、创建向量场:均匀采样的情况下,假设划分的块是常量,通过向量场V逼近指示函数的梯度。采用三次条样插值(三线插值);
4、求解泊松方程:方程的解采用拉普拉斯矩阵迭代求出;
5、提取等值面:为得到重构表面,需要选择阈值获得等值面;先估计采样点的位置,然后用其平均值进行等值面提取,然后用移动立方体算法得到等值面。