按照惯例,先给结论:
(1)1985国家高程基准与EGM2008的差异有严密的理论公式计算;
(2)1985国家高程基准与EGM20008的垂直偏差与参考系、水准模型、选取的水准点有关系
(3)选用CGCS2000、EGM2008和全国936个GPS水准点,得出我国高程基准比全球大地水准面高0.32m
《不同高程基准位差计算的严密理论研究_张利明》
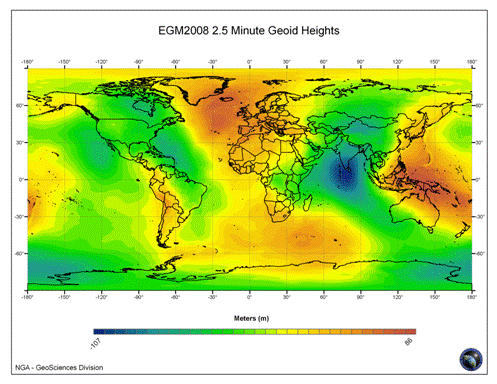
高程基准是高程测定的依据, 其对构建“ 数字地球” 、研究区域性环境变化以及海面地形等方面具有重要的科学和现实意义. 长期以来人们一直把平均海水面作为高程起算面. 这个高程起算面的确定一般是由一个或多个验潮站在一定时期内的观测数据通过某种形式的平均得到. 但由于海面地形客观存在, 并且各个国家的验潮站位置和观测时间不同以及数据处理方式不同等原因, 这样由一个或多个验潮站确定的高程基准其实是一种局部高程基准, 这使得许多国家或地区的高程基准面存在差异( 不同高程基准之间系统差), 甚至同一国家或地区不同时期的验潮资料确定的高程基准也不完全相同.就海面地形困一项的影响而言, 这种差异在全球范围内最大可达2m 之多. 这个差异已经严重影响了地球信息数据的全球共享机制. 事实上, 许多学者已经注意到了高程基准的不统一问题.
本文通过严密分析高程基准与重力位之间的关系, 推导其在正高系统和正常高系统的严密计算公式, 为我们研究全球高程基准的统一提供理论支持.
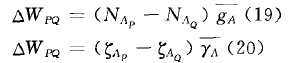 平均重力和平均正常重力
平均重力和平均正常重力
从以上的理论推导可以得出, 不管是在正高系统还是正常高系统中, 如果知道任意点A 在不同基准中的正高或大地水准面高以及正常高或高程异常, 都可以计算出不同高程基准之间的位差, 同时我们可以根据Bruns公式计算出两个基准在地球上任意点的垂直偏差.
本文利用重力位的相关理论, 结合高程基准的定义, 基于正高和正常高两个不同高程系统, 分别推导了正高系统、正常高系统以及两者之间的高程基准位差严密计算公式, 同时给出了毫米级精度下的近似计算公式.该理论为构建全球高程基准统一模型提供了依据, 尤其在利用卫星重力提供全球统一尺度基准( 例如低阶地球重力场模型) 的条件下, 为利用G P S / 重力边值问题统一全球高程基准奠定了基础.
《利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差_翟振和》
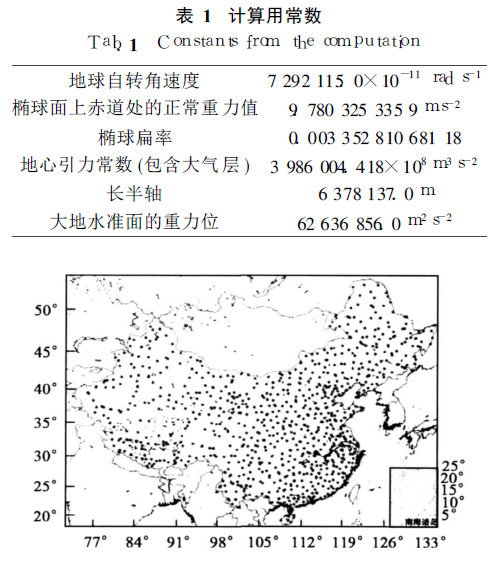
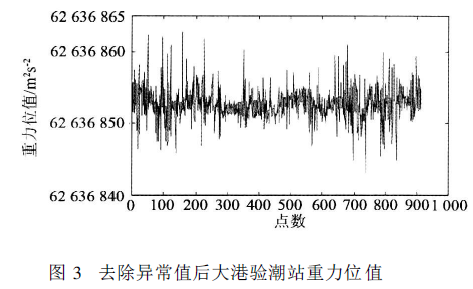
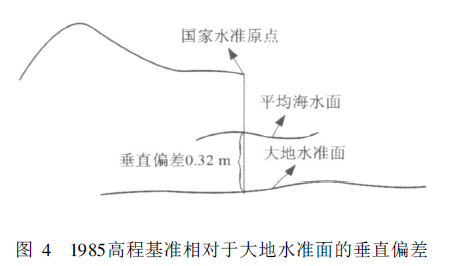
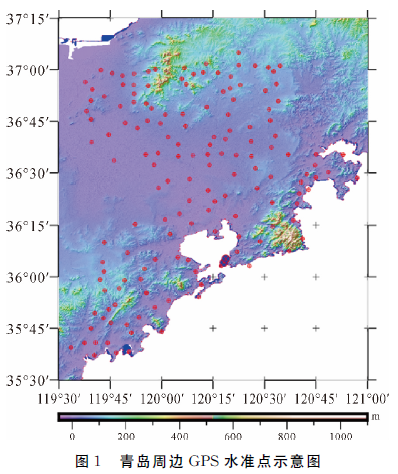
高程基准面相对于大地水准面的垂直偏差是区域高程基准转换和全球高程基准统一的基础数据。利用最新发布的EGM2008地球重力场模型和中国均匀分布的936个GPS水准点数据计算得出中国青岛大港验潮站的重力位为62 636 852.85 ±0.07 m2 /s2, 进而得到中国1985高程基准相对大地水准面的垂直偏差为0.32 m。
下图是CGCS2000坐标系统,以及选取的水准点
利用重力位差的思想计算得到了我国高程基准相对于大地水准面的垂直偏差。利用最新发布的EGM2008地球重力场模型并结合我国均匀分布的936个GPS水准点数据得到了我国青岛大港验潮站的重力位为62 636 852.85 ±0.07 m2 /s2, 进而得到我国高程基准相对全球大地水准面间的偏差为0.32m。由于高程基准垂直偏差的计算受GPS水准点和位模型影响较大, 因此未来建议采用更多高等级的GPS水准点数据, 同时采用更高精度的引力位模型,以便得到更精确的数值结果。
《1985国家高程基准与全球似大地水准面在广东地区的垂直偏差_许耿然》
1) 本文利用重力位差原理,通过抗差等价权计算了广东地区85 高程与全球高程的垂直偏差。结果表明,二者在广东地区的垂直偏差接近全国平均偏差,为32.3 cm。
2) 对几个具有代表性的地球重力场模型及简单组合模型进行了比对分析。结果表明,在整个广东地区,EGM2008 / EIGEN-6C 模型的精度最高,中误差为7.5 cm,说明EGM2008 /EIGEN-6C 与广东地区大地水准面最为吻合。
3) 由中分辨率地球重力场模型及其与EGM2008 的组合模型可以得出,其低阶位系数精度一般较高,若需要使用这些模型,建议对低于2160阶的模型都用EGM2008 模型位系数进行补充,以提高模型的分辨率。
4) 对于广东这种局部区域得到的1985 高程验潮站重力位值,可为该地区利用重力位差进行远距离海岛( 礁) 跨海高程传递提供参考,可为即将开展的广东海洋经济综合试验区测绘地理信息工程海洋测绘基准的建设提供新的高程传递方案。
《区域与全球高程基准差异的确定_李建成》
高程基准是国家或地区表示地形高程的起算依据,一般由一个水准基面和一个永久性水准原点组成。水准基面是高程为零的起算面,一般是过高程零点的大地水准面或似大地水准面。但水准原点一般不是高程零点,而是实际水准测量高程的起算点。水准原点的高程通常是将验潮站的平均海面作为“零”基准起算通过精密水准测量获得,而精密水准测量是通过几何水准高差和沿水准路线的重力位差进行高程传递。由于水受到地球引力作用往低处流,因而将海面作为高程零起算面符合人们对自然现象的直观认识,传统上就是以海平面为依据定义高程基准。具体实施时要利用沿海单个或多个验潮站多年的潮位观测资料,通过一定原理和方法求取平均海面作为高程基准的零点。例如,我国1985高程基准是以青岛单验潮站的平均海面为高程零点,北美垂直基准是以加拿大魁北克里穆斯基的局部平均海面作为北美高程零点,欧洲统一高程基准是以荷兰阿姆斯特丹的单个验潮站的平均海面为高程零点,韩国是以韩国半岛东北边仁川湾验潮站观测的平均海面作为韩国高程零点。而澳大利亚1971年高程基准是以澳大利亚沿岸30个验潮站的平均海面作为澳大利亚的高程零点,也就是30个验潮站的高程都为零。
显然,由于全球各地平均海面的大地高不同,因此不同国家或地区间的高程基准面也不相同,这影响和制约了全球空间信息的共享与交换,例如,长距离水调工程、油气输送管网工程、跨境跨国高速公路、铁路等线路工程建设中,需要统一的高程信息,否则无法确保工程项目的联合施工作业与对接。欧洲多年来一直在建设欧洲统一水准网和欧洲垂直参考网,目的就是试图统一欧洲高程基准,南美洲也在全球统一高程系统框架内开展南美洲垂直参考系统SIRGAS(Sistema de Referencia Geocéntrico para las Américas)的定义与实现。统一全球高程参考系统已经成为全球大地测量观测系统一体化(IGGOS:Integrated Global Geodetic Observation System)的基础任务之一。
针对高程基准的统一问题,文献[6]指出,只要基于不同高程基准的两个水准点的高程值已知,且可用水准联测,那么这两个高程基准完全可以连接统一。如果两个高程基准之间无法用水准联测,则可以基于位理论原理,借助全球重力场模型,进行高程基准统一。国外很多学者早就开展了卓有成效的研究,在理论方法和数值结果方面取得许多有重要参考价值的成果。文献[7]计算了英国、德国、美国和澳大利亚几个国家高程基准与全球大地水准面的差异;文献[8-9]计算了波罗的海周边国家的高程基准重力位;文献[10]计算了瑞典与芬兰两国高程基准间的垂直差异;文献[11]计算了澳大利亚高程基准、北美垂直基准与全球高程基准间的位差及垂直差异;文献[2]计算了韩国高程基准与全球基准间的基准差异。事实上,一个国家陆地与远距离岛屿之间的跨海高程传递,其本质上也是一种高程基准统一问题。例如,文献[12]在将黄海高程由陆地传递到距离上海芦潮港30 km的洋山岛时,将小洋山的潮位资料计算的平均海面与GPS水准引测高程计算的平均海面比较,实现了岛屿高程与陆地高程基准的统一。
考虑到国家或地区间尤其是洲际间水准测量联测难以甚至无法实施,目前高程基准统一连接一般是联合全球重力场模型和GPS水准数据,计算不同基准间的重力位差或者直接计算基准几何差异。位差法是利用重力场模型和GPS水准点的位置信息,计算局部区域水准点的重力位,再根据水准观测的海拔高程,反算水准点相对于高程零点的位差或大地位数,进而得到高程零点重力位。最后结合选取的全球基准重力位,得到局部基准与全球基准的位差,进而转换成基准差异。事实上,对于两个区域高程基准,分别利用各基准下的GPS水准数据,计算两个区域高程基准零点重力位,就可以根据位差法实现两个区域高程基准的统一连接。几何差异法一般称为高程异常差法或者大地水准面高差法,是利用重力场模型和GPS观测信息,计算得到“重力”高程异常(或大地水准面)。同时,将GPS大地高减去水准海拔高,得到“几何”高程异常(或大地水准面),两个高程异常(或大地水准面)之差反映了高程基准间的差异。由全球重力场模型计算高程异常(或大地水准面)时,已经默认了正常重力位U0所表示的大地水准面作为全球高程基准面,因此,几何差异法一般用于区域基准与全球基准的统一连接。
从1985国家高程基准建立开始,国内学者一直都在研究和讨论我国高程基准与全球高程基准的差异问题。早在1989年,文献[17]就利用全国一等水准资料,联合近海验潮站的水准联测高程,推算了中国近海平均海面相对于1985国家高程基准的高程,得出了中国近海平均海面呈现“南高北低”(请看本网站的http://www.xiaokcehui.com/?post=240)的结论。采用海洋学的方法,利用海水密度、温盐资料也可以得出我国沿海平均海面这种特点。这些结果说明采用青岛单个验潮站资料建立的1985高程基准面与我国沿海地区平均海面存在偏差,与全球平均海面同样也存在偏差。前面论述的位差法、高程异常差法和海洋学方法,都在确定我国高程基准与全球基准方面得到了实际应用,由于选取的全球高程基准并不完全一致,因此推算的我国高程基准与全球基准的差异在22~46 cm之间。
目前,大地测量领域常用异常位法、正常高反算法、高程异常差法确定高程基准差异[13-16],3种方法虽然实现上有区别,但其实质都是利用物理大地测量学中位理论和高程系统定义推导得到,其在模型上并未完全统一。本文从高程基准差异的定义出发,推导现有3种方法的统一数学模型,探讨各种方法的关联性和区别;分析大地测量参考系和椭球参数对确定高程基准差异的影响;最后基于我国实测GPS和水准资料,确定我国85高程基准与全球高程基准的差异,并针对区域高程基准与全球高程间基准差异的确定给出几个结论和建议。
本文从经典高程系统确定的理论和定义出发,给出了不同区域和全球高程基准差异的定义,并推导可将现有3种方法统一的数学模型。基于此,探讨了计算区域与全球高程基准差异需要考虑的几个问题,包括全球高程基准的选择、大地参考系和椭球参数对确定高程基准差异的影响等问题。最后,由我国青岛周边实测GPS水准资料及全球超高阶重力场模型,确定了我国85高程基准与全球高程基准的差值。主要有以下几个结论和建议:
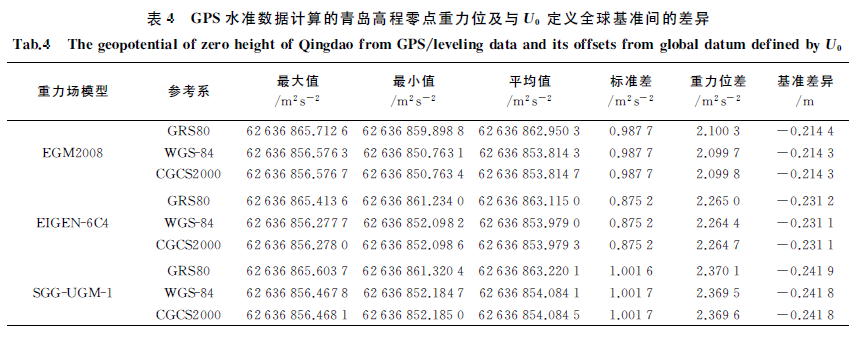
(1) 本文将当前用于高程基准统一的3种方法进行了统一,不同高程基准间的基准差异均可定义为基准之间的位差与平均重力或平均正常重力比值的形式,确定位差时不依赖于采用的高程系统,确保了差值的唯一性。实际数值结果(表 4与表 6,表 5与表 7)进一步证明了3种方法的计算结果之间的差异可以忽略。
(2) 在高程基准比较时,必须要考虑不同参考系参考椭球参数的影响。特别是在涉及重力位时,不同重力位值的比较必须在相同参考系下进行,否则没有意义。利用地球引力位模型计算重力位或其他相关的重力场参量,需要按照式(11) 进行位系数的转换,其本质等同于选定参考系,数值结果都是针对于选定参考系的。
(3) 在根据大地水准面或高程异常计算基准差异时,除了按照式(11) 转换位系数之外,还要考虑全球大地水准面重力位与参考椭球正常重力位的差异,这就是零阶项的问题。例如早期用EGM96模型在WGS-84下计算大地水准面时,需要加上-53 cm的零阶项改正[37],以及用最新的EGM2008模型在WGS-84下计算大地水准面时,需要加上-41 cm改正。本文利用全球平均海面作为全球高程基准,此时的全球高程基准重力位与选择参考椭球的正常重力位U0不等,产生的零阶项影响约为-44 cm(表 7),与当前EGM2008模型给出的41 cm数值接近。
(4) 综合本文的理论推导和数值结果与分析,可以得出我国1985国家高程基准的总体情况:当选取GRS80、WGS-84、CGCS2000参考系正常重力位U0所定义大地水准面作为全球高程基准时,基于青岛原点152个水准点和EIGEN-6C4模型,得到我国1985高程基准低于全球高程基准约23.1 cm;当选取全球平均海面的平均重力位定义全球高程基准时,我国1985高程基准高于全球基准约21.0 cm。因此我国高程基准与全球基准之差,主要取决于全球基准位的选择和所使用的GPS水准观测数据。国内关于我国高程基准差异数值结果的不同,其主要差别就在于全球基准面选择和所采用的GPS水准观测数据不同。
(5) 计算区域与全球高程基准差异时,应该选择距离区域高程基准零点较近的GPS水准数据。一方面水准传递误差小,另一方面,重力场模型在小范围区域内的精度差异较小,因此,选择青岛周边GPS水准资料。从青岛152个GPS水准数据与全球重力场模型计算高程异常的差异看出,当前重力场模型在青岛周边不同点的精度差别依然较大,导致选择不同区域数据对确定我国1985国家高程基准与全球基准差异的影响较大。例如,本文的结果与早期使用青岛周边65个GPS水准数据联合EGM2008计算的基准差异有7.1 cm的不同,也说明了同样的问题。因此,如要实现厘米级精度的区域与全球高程基准统一,目前全球重力场模型的精度还不能满足要求。但是,随着时频测量技术发展及精度的不断提高,利用时频观测重力位及位差的方法有望用于高程基准的统一。
geographiclib库
geographiclib是一个开源库,它的网址https://geographiclib.sourceforge.io/,它提供了查询水准面、重力异常和地球磁场强度的代码库和数据。OpenCoord最好将这个库融合进去,提供了全球水准异常、重力和磁力异常数据的查询和提取。这个作为未来2-3年的任务。
最后发福利,EGM2008-1分的水准面模型和对应的GUI在如下连接:
链接:https://pan.baidu.com/s/1Vz8v3nZYLByroeELgd6YBw
提取码:1hul