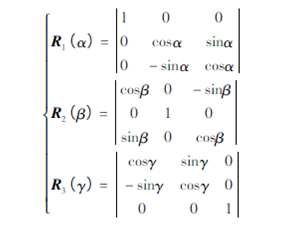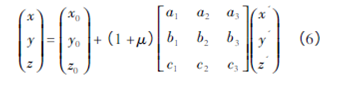摘要:出于对目前常用的两种坐标系转换模型的学习和理解,对原本适合于小角度坐标转换的布尔莎模型进行了拓展, 使其适合于任意角度坐标转换。将改进后的7 参数布尔莎模型与13 参数的大角度模型,结合盾构三棱镜法解算盾首盾 尾坐标的工程实例,通过大旋转角和小旋转角两组数据以及编程实现两者的对比,并得出了结论。
重要表述:
需要特别指出的是: 由于布尔莎模型对式( 2)中的三角函数作了近似处理,所以在应用上受到了限制,只能适合于小角度的坐标转换。
与7 参数模型类似, 13 参数的思路是将7 参数模型中R1( α) R2( β) R3( γ) 3 个相乘的旋转矩阵用R 阵代替,R 阵中包含有9 个参数都设为未知参数a1、a2、a3、b1、b2、b3、c1、c2、c3,再加上一个尺度参数μ和3 个平移参数x0、y0、z0一共是13 个参数。
经过编程解算,结果显示: 7 参数模型和13 参数模型解算出的平移参数和尺度参数在10 - 6 级以上,分别解算出的R 阵9 个元素间在10 - 10级上都完全相同,即在指定限差内,小角度坐标系转换和大角度坐标系转换迭代解算出的转换参数几乎完全一致。
如果允许α 与sinα 之差在0. 000 5 弧度以内认为是相同的,则可利用式( 13) 中约等号右端的近似R 阵列立误差方程,这便是布尔莎模型的思路,可看作是满足特定条件下的简化方程,本例小角度数据中的最大角γ 满足γ - sinγ = 0. 000 208 545 7 <
0.000 5,则可用布尔莎模型解算,
结论:
两种参数模型解算过程中迭代次数不同的原因,主要是由于7 参数模型是用多余两个方程平差解算7 个参数,而13 参数模型同样是利用多余两个方程却平差解算13 个参数,多余观测数所占总的方程比例7 参数模型比13 参数模型占优。总体来说,无论是7 参数模型还是13 参数模型,都可以解决任意角度坐标系转换的问题,7参数模型参数少,但线性方程不好列; 13 参数模型线性方程比较容易列出,但参数过多,计算时内存占用更大,不如7 参数效率高。